rearrange() your correlations with corrr
Don’t stare at your correlations in search of variable clusters when you can rearrange() them:
library(corrr)
mtcars %>% correlate() %>% rearrange() %>% fashion()
#> rowname am gear drat wt disp mpg cyl vs hp carb qsec
#> 1 am .79 .71 -.69 -.59 .60 -.52 .17 -.24 .06 -.23
#> 2 gear .79 .70 -.58 -.56 .48 -.49 .21 -.13 .27 -.21
#> 3 drat .71 .70 -.71 -.71 .68 -.70 .44 -.45 -.09 .09
#> 4 wt -.69 -.58 -.71 .89 -.87 .78 -.55 .66 .43 -.17
#> 5 disp -.59 -.56 -.71 .89 -.85 .90 -.71 .79 .39 -.43
#> 6 mpg .60 .48 .68 -.87 -.85 -.85 .66 -.78 -.55 .42
#> 7 cyl -.52 -.49 -.70 .78 .90 -.85 -.81 .83 .53 -.59
#> 8 vs .17 .21 .44 -.55 -.71 .66 -.81 -.72 -.57 .74
#> 9 hp -.24 -.13 -.45 .66 .79 -.78 .83 -.72 .75 -.71
#> 10 carb .06 .27 -.09 .43 .39 -.55 .53 -.57 .75 -.66
#> 11 qsec -.23 -.21 .09 -.17 -.43 .42 -.59 .74 -.71 -.66
This post will explain how you can get the most from rearrange() for exploring correlations when using the corrr package.
Why rearrange? #
It might seem obvious to some, but let’s first think about why we might rearrange our correlations. The main reason for this is that we should always be looking at our correlations, regardless of the models we ultimately employ on the data. This is because many of our most commonly used models are methods for reducing or reinterpreting a correlation matrix (regression is a perfect example). So, while sophisticated models are useful and important, we should always be looking at the correlations. For example, looking at the correlations is an effective way to locate multicollinearity problems. Model results can be misleading if we’re not familiar with the underlying correlations. So looking at correlations is important, and the purpose of rearranging them based on their clustering is to make life easier for ourselves: to more easily see patterns in the data, spot oddities, etc.
What does rearrange() do? #
rearrange() is a function provided in the corrr package. Like most functions from corrr, it takes a correlation data frame (cor_df) as it’s first argument. This is created using correlate():
d <- correlate(mtcars)
d
#> # A tibble: 11 x 12
#> rowname mpg cyl disp hp drat
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mpg NA -0.8521620 -0.8475514 -0.7761684 0.68117191
#> 2 cyl -0.8521620 NA 0.9020329 0.8324475 -0.69993811
#> 3 disp -0.8475514 0.9020329 NA 0.7909486 -0.71021393
#> 4 hp -0.7761684 0.8324475 0.7909486 NA -0.44875912
#> 5 drat 0.6811719 -0.6999381 -0.7102139 -0.4487591 NA
#> 6 wt -0.8676594 0.7824958 0.8879799 0.6587479 -0.71244065
#> 7 qsec 0.4186840 -0.5912421 -0.4336979 -0.7082234 0.09120476
#> 8 vs 0.6640389 -0.8108118 -0.7104159 -0.7230967 0.44027846
#> 9 am 0.5998324 -0.5226070 -0.5912270 -0.2432043 0.71271113
#> 10 gear 0.4802848 -0.4926866 -0.5555692 -0.1257043 0.69961013
#> 11 carb -0.5509251 0.5269883 0.3949769 0.7498125 -0.09078980
#> # ... with 6 more variables: wt <dbl>, qsec <dbl>, vs <dbl>, am <dbl>,
#> # gear <dbl>, carb <dbl>
For more details about corrr and correlate(), view the package README file, also posted HERE.
We can now rearrange this correlation data frame with rearrange():
rearrange(d)
#> # A tibble: 11 x 12
#> rowname am gear drat wt disp
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 am NA 0.7940588 0.71271113 -0.6924953 -0.5912270
#> 2 gear 0.79405876 NA 0.69961013 -0.5832870 -0.5555692
#> 3 drat 0.71271113 0.6996101 NA -0.7124406 -0.7102139
#> 4 wt -0.69249526 -0.5832870 -0.71244065 NA 0.8879799
#> 5 disp -0.59122704 -0.5555692 -0.71021393 0.8879799 NA
#> 6 mpg 0.59983243 0.4802848 0.68117191 -0.8676594 -0.8475514
#> 7 cyl -0.52260705 -0.4926866 -0.69993811 0.7824958 0.9020329
#> 8 vs 0.16834512 0.2060233 0.44027846 -0.5549157 -0.7104159
#> 9 hp -0.24320426 -0.1257043 -0.44875912 0.6587479 0.7909486
#> 10 carb 0.05753435 0.2740728 -0.09078980 0.4276059 0.3949769
#> 11 qsec -0.22986086 -0.2126822 0.09120476 -0.1747159 -0.4336979
#> # ... with 6 more variables: mpg <dbl>, cyl <dbl>, vs <dbl>, hp <dbl>,
#> # carb <dbl>, qsec <dbl>
Notice how the strongest correlations are closest to the diagonal, while the weakest are further away. This is the main purpose of rearrange(), which helps to find variable clusters and so on.
How is the order decided? #
To do this, rearrange() depends on seriate() from the seriation package. seriate() “tries to find an linear order for objects”. So the correlations are submitted to seriate() to find the order to rearrange them.
Changing the method #
Because of seriate(), rearrange() provides the method argument, which allows us to specify the arrangement (clustering) method. The help page for ?seriate() provides the full list of possible methods. Here’s a quick example:
rearrange(d) # the default is PCA (Principal Component Analysis).
#> # A tibble: 11 x 12
#> rowname am gear drat wt disp
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 am NA 0.7940588 0.71271113 -0.6924953 -0.5912270
#> 2 gear 0.79405876 NA 0.69961013 -0.5832870 -0.5555692
#> 3 drat 0.71271113 0.6996101 NA -0.7124406 -0.7102139
#> 4 wt -0.69249526 -0.5832870 -0.71244065 NA 0.8879799
#> 5 disp -0.59122704 -0.5555692 -0.71021393 0.8879799 NA
#> 6 mpg 0.59983243 0.4802848 0.68117191 -0.8676594 -0.8475514
#> 7 cyl -0.52260705 -0.4926866 -0.69993811 0.7824958 0.9020329
#> 8 vs 0.16834512 0.2060233 0.44027846 -0.5549157 -0.7104159
#> 9 hp -0.24320426 -0.1257043 -0.44875912 0.6587479 0.7909486
#> 10 carb 0.05753435 0.2740728 -0.09078980 0.4276059 0.3949769
#> 11 qsec -0.22986086 -0.2126822 0.09120476 -0.1747159 -0.4336979
#> # ... with 6 more variables: mpg <dbl>, cyl <dbl>, vs <dbl>, hp <dbl>,
#> # carb <dbl>, qsec <dbl>
rearrange(d, method = "HC") # Method changed to Hierarchical Clustering
#> # A tibble: 11 x 12
#> rowname hp vs qsec carb wt
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 hp NA -0.7230967 -0.70822339 0.74981247 0.6587479
#> 2 vs -0.7230967 NA 0.74453544 -0.56960714 -0.5549157
#> 3 qsec -0.7082234 0.7445354 NA -0.65624923 -0.1747159
#> 4 carb 0.7498125 -0.5696071 -0.65624923 NA 0.4276059
#> 5 wt 0.6587479 -0.5549157 -0.17471588 0.42760594 NA
#> 6 cyl 0.8324475 -0.8108118 -0.59124207 0.52698829 0.7824958
#> 7 mpg -0.7761684 0.6640389 0.41868403 -0.55092507 -0.8676594
#> 8 disp 0.7909486 -0.7104159 -0.43369788 0.39497686 0.8879799
#> 9 drat -0.4487591 0.4402785 0.09120476 -0.09078980 -0.7124406
#> 10 am -0.2432043 0.1683451 -0.22986086 0.05753435 -0.6924953
#> 11 gear -0.1257043 0.2060233 -0.21268223 0.27407284 -0.5832870
#> # ... with 6 more variables: cyl <dbl>, mpg <dbl>, disp <dbl>, drat <dbl>,
#> # am <dbl>, gear <dbl>
Using absolute values #
The third and, currently, final argument of rearrange() is absolute. This boolean argument specifies whether the absolute values for the correlations should be used for clustering or not. If TRUE, then rearrange() will use absolute values of the correlations to determine their order, thus ignoring correlation signs. absolute = TRUE by default as I consider the magnitude of the correlations to be more important than their signs when exploring for patterns. However, we can override this, forcing more negative correlations to be further from the diagonal line than more positive correlations as follows:
rearrange(d, absolute = FALSE)
#> # A tibble: 11 x 12
#> rowname mpg vs drat am gear
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 mpg NA 0.6640389 0.68117191 0.59983243 0.4802848
#> 2 vs 0.6640389 NA 0.44027846 0.16834512 0.2060233
#> 3 drat 0.6811719 0.4402785 NA 0.71271113 0.6996101
#> 4 am 0.5998324 0.1683451 0.71271113 NA 0.7940588
#> 5 gear 0.4802848 0.2060233 0.69961013 0.79405876 NA
#> 6 qsec 0.4186840 0.7445354 0.09120476 -0.22986086 -0.2126822
#> 7 carb -0.5509251 -0.5696071 -0.09078980 0.05753435 0.2740728
#> 8 hp -0.7761684 -0.7230967 -0.44875912 -0.24320426 -0.1257043
#> 9 wt -0.8676594 -0.5549157 -0.71244065 -0.69249526 -0.5832870
#> 10 disp -0.8475514 -0.7104159 -0.71021393 -0.59122704 -0.5555692
#> 11 cyl -0.8521620 -0.8108118 -0.69993811 -0.52260705 -0.4926866
#> # ... with 6 more variables: qsec <dbl>, carb <dbl>, hp <dbl>, wt <dbl>,
#> # disp <dbl>, cyl <dbl>
Pairing with output functions #
I tend to use rearrange() as a precursor to one of the output functions provided by corrr. For example, use fashion() to print them to the screen, or rplot() to visualise them.
d %>% rearrange() %>% fashion()
#> rowname am gear drat wt disp mpg cyl vs hp carb qsec
#> 1 am .79 .71 -.69 -.59 .60 -.52 .17 -.24 .06 -.23
#> 2 gear .79 .70 -.58 -.56 .48 -.49 .21 -.13 .27 -.21
#> 3 drat .71 .70 -.71 -.71 .68 -.70 .44 -.45 -.09 .09
#> 4 wt -.69 -.58 -.71 .89 -.87 .78 -.55 .66 .43 -.17
#> 5 disp -.59 -.56 -.71 .89 -.85 .90 -.71 .79 .39 -.43
#> 6 mpg .60 .48 .68 -.87 -.85 -.85 .66 -.78 -.55 .42
#> 7 cyl -.52 -.49 -.70 .78 .90 -.85 -.81 .83 .53 -.59
#> 8 vs .17 .21 .44 -.55 -.71 .66 -.81 -.72 -.57 .74
#> 9 hp -.24 -.13 -.45 .66 .79 -.78 .83 -.72 .75 -.71
#> 10 carb .06 .27 -.09 .43 .39 -.55 .53 -.57 .75 -.66
#> 11 qsec -.23 -.21 .09 -.17 -.43 .42 -.59 .74 -.71 -.66
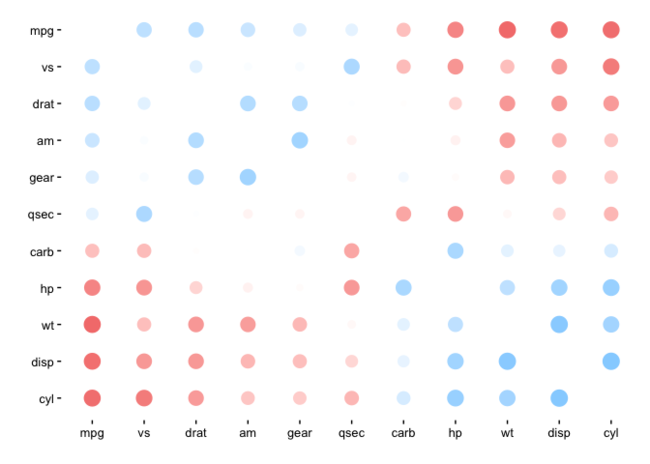
d %>% rearrange(absolute = FALSE) %>% rplot()
# Squeeze in shave() for an even cleaner look
d %>% rearrange() %>% shave() %>% fashion()
#> rowname am gear drat wt disp mpg cyl vs hp carb qsec
#> 1 am
#> 2 gear .79
#> 3 drat .71 .70
#> 4 wt -.69 -.58 -.71
#> 5 disp -.59 -.56 -.71 .89
#> 6 mpg .60 .48 .68 -.87 -.85
#> 7 cyl -.52 -.49 -.70 .78 .90 -.85
#> 8 vs .17 .21 .44 -.55 -.71 .66 -.81
#> 9 hp -.24 -.13 -.45 .66 .79 -.78 .83 -.72
#> 10 carb .06 .27 -.09 .43 .39 -.55 .53 -.57 .75
#> 11 qsec -.23 -.21 .09 -.17 -.43 .42 -.59 .74 -.71 -.66
Sign off #
Thanks for reading and I hope this was useful for you.
For updates of recent blog posts, follow @drsimonj on Twitter, or email me at drsimonjackson@gmail.com to get in touch.
If you’d like the code that produced this blog, check out my GitHub repository, blogR.